HOMOTECIA
EXPERIMENTA
HOMOTECIA
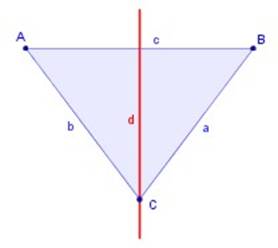
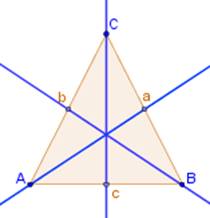
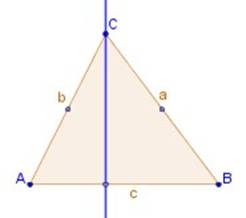
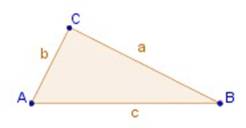
Es la transformación geométrica que no tiene una imagen congruente, ya que a partir de una figura dada se obtienen una o var9ias figuras en tamaño mayor o menor que la figura dada, para obtenerlas se parte de un punto escogido arbitrariamente, al cual se llama centro de homotecia, del cual se trazan segmentos de recta, tantos como vértices tenga la figura que se va a transformar, se debe considerar otro elemento básico para desarrollar esta transformación, siendo esta una constante, la cual se denomina constante de homotecia que viene a ser la escala en la cual se realiza la reproducción.
Tiene las siguientes propiedades:
- Los ángulos de las figuras por homotecia son iguales ya que tienen la misma medida.
- Los segmentos con paralelos.
- Las dimensiones de dos figuras por homotecia son directamente proporciónales; esta proporción es fijada por la constante de homotecia.
Aquellas figuras que no cumplen con la propiedad de ser paralelos los segmentos se les denomina figuras semejantes, a las que cumplen con todas las propiedades se les denomina figuras homoteticas.
En una homotecia de centro el punto O y razón k:
- Si k > 0, A y A′ están al mismo lado de O, y se dice que la homotecia es directa.
- Si k < 0, A y A′ están a distinto lado de O, y se dice que la homotecia es inversa.
A la figura ABCD le hemos aplicado una homotecia de centro O y razón k, con k > 0; homotecia directa.
A la figura ABC le hemos aplicado una homotecia de centro O y razón k, con k < 0; homotecia inversa.



 Y ¿cómo se busca el centro de rotación? CENTRO de ROTACION: Se toma el punto medio entre A y A’ y se dibuja allí la simetral. Se toma el punto medio entre B y B’ y se dibuja allí la simetral. El punto de intersección es O.
Y ¿cómo se busca el centro de rotación? CENTRO de ROTACION: Se toma el punto medio entre A y A’ y se dibuja allí la simetral. Se toma el punto medio entre B y B’ y se dibuja allí la simetral. El punto de intersección es O.

 Y Resumiendo:
Y Resumiendo:
 Cuando se habla de trasladar figuras geométricas, sean bidimensionales o tridimensionales, en el espacio, es común que surjan complicaciones cuando entran en juego conceptos como la
Cuando se habla de trasladar figuras geométricas, sean bidimensionales o tridimensionales, en el espacio, es común que surjan complicaciones cuando entran en juego conceptos como la